Division Decisions

In Math Workshop, we have been working to connect division to multiplication. Many times, we even find ourselves thinking of division problems as multiplication problems so that we can use a multiplication strategy to solve them.
Consider 56 divided by 4

When looking at this division problem, we ask ourselves, “How many 4’s are in 56?”. By doing this, we recognize that we will be finding the number of groups of 4 that are in 56, or _____ x 4 = 56.

Decisions, decisions. What strategy should be used?

Many students find it simple to use an efficient form of Skip-Counting by multiples of 4 to determine the answer. Starting with the 10th multiple of 4 would be very common. The answer is 14. It takes 14 groups of 4 to equal 56.

Other students would incorporate this same strategy into a different model, such as a Multiplication Cluster. The approach uses decomposition of one of the factors to make smaller, easier probloems. In the example below, again 14 is decomposed into 10 and 4 to make the two easier problems. 10 groups of 4 is 40. Adding another 4 groups of 4 (4x4) or 16 “builds” 14 x 4 = 56. 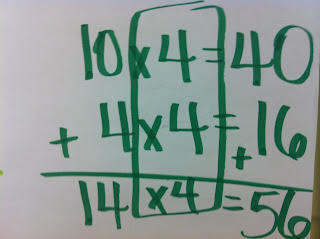56 divided by 4 can also be thought of as 56 divided by 2, and again divided by 2 (dividing by 2 twice is the same as dividing by 4). Some students like to refer to this strategy as the “Halfsie-Halfsie”. 56 divided by 2 is 28. 28 divided by 2 is 14. This strategy only works when 4 is the divisor.

A more advanced strategy would be to take the dividend (total) and decompose it into smaller multiples of the divisor to make smaller division problems that would “build “ (add up to) the original division problem. This method is called a Division Cluster. 56 could be decomposed into 20 + 20 + 16 and solved as three smaller division problems. 20 divided by 4 is 5. 20 divided by 4 is 5. 16 divided by 4 is 4. 56 divided by 4 is 14.

Last but not least, the Partial Quotients Method (also lovingly referred to as the “Russian Peasant” Method), is a special model we move our students toward in order to progress their thinking into a more “standard algorithmic” set-up. If you look carefully at the smaller problems that are solved in each of the examples shown below, you will see that they are the same as in the earlier examples. Even though the mathematical “models” are different, the “strategy” of using good mathematical sense to decompose the dividend into smaller numbers (landmark multiples of ten or single digit numbers) is the same, so that the reasonableness of solutions can be easily assessed (Does my answer make sense?).
Our approach is a conceptual-based approach, teaching students that there is a relationship between multiplication and division and there is a meaning as to the dividend, divisor, and quotient. One represents the total (dividend) and the other two parts represent the number of groups and the size of the groups that make up the total.

These are just a sampling of the more common strategies our students are currently using in the classroom to solve division problems. Students often find themselves creating their own unique ways of approaching division problems in addition to those shown here. :-)
Promoting this deep understanding at Grade 4 will then more easily transfer later (5th Grade) into understanding why the division algorithm works (which is very abstract in nature and cumbersome to understand conceptually).

Happy Dividing!
P.S.- Students, leave a comment sharing your favorite divison strategy (and why), and earn Behavior Bucks to spend at your next class auction!